El documento pionero de Diffie y Hellman "Multiuser Cryptographic Techniques." introdujo un nuevo enfoque de la criptografía y desafió a los criptólogos a elaborar un algoritmo criptográfico que cumpliera los requisitos de los sistemas de clave pública. Una de las primeras respuestas al desafío fue desarrollada en 1977 por Ron Rivest, Adi Shamir y Len Adleman en el MIT y publicada por primera vez en 1978. Desde entonces, el esquema de Rivest-Shamir-Adleman (RSA) ha reinado como el enfoque de uso general más ampliamente aceptado e implementado para el cifrado de clave pública.

---

Diagrama

Comunicación con criptografía asimétrica

---

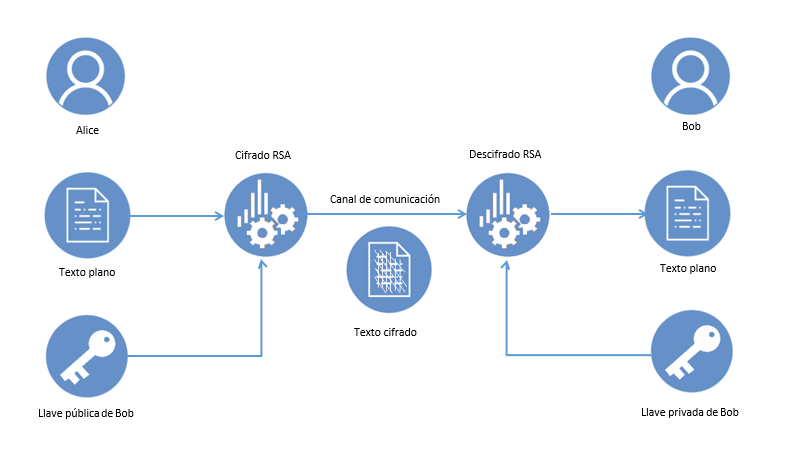
Cifrado

Si Alice quiere enviarle un mensaje m a Bob.

1. Bob selecciona dos grandes números primos distintos p y q y los multiplica para formar n = p * q.
2. Bob también elige un exponente de cifrado e tal que MCD (e, (p — l), (q — 1)) = 1.
3. Bob envía la pareja de valores (n , e) a Alice pero mantiene los valores de p y q secretos.
4. Alice convierte el mensaje m en un entero tal que 0 ≤ m < n. Si m es mayor, se divide en bloques más pequeños. Se utiliza cualquier método para la conversión.
5. Alice calcula c ≡ m^e mod n.
6. Alice envía el texto cifrado c a Bob.

---

Descifrado

1. Bob recibe el texto cifrado c de Alice.
2. Puesto que Bob conoce p y q, puede calcular (p - 1)(q - 1) y por lo tanto puede encontrar el exponente de descifrado d con de ≡ 1 mod (p - 1)(q - 1).
3. Bob realiza el cálculo m ≡ c^d mod n.
4. Bob realiza la conversión de m a texto.

Por ejemplo:

Alice		Bob
m = 4		p = 3, q = 11 -> n = 33
	e = 3
	<--- (33 , 3)
c ≡ 43 mod 33
	31 --->
		c = 31
		d ≡ e-1 ≡ 7 mod (3-1)(11-1)
		m = 317 ≡ 4 mod 33

---

Referencias

1. Trappe, W., Washington, L. (2006). The RSA Algorithm. En Introduction to Cryptography with Coding Theory(164-169). United States of America: Prentice Hall.