Obtención de puntos

La curva elíptica con la que trabajaremos es:
Para el uso criptográfico, tenemos que considerar la curva no sobre los números reales sino sobre un campo finito. La opción más popular son los campos primos , donde toda la aritmética se hace módulo un primo . Es por esto que se eligió el número ya que es primo. Los coeficientes y deben satisfacer que primero pertenezcan al campo primo, en este caso, y que , verificamos lo anterior, y , ambos están en el campo y
por lo tanto tenemos una curva elíptica válida.
Obtener puntos
Como se explica en la teoría, se necesita de un punto que pertenezca a la curva para realizar las operaciones, a este punto se le conoce como punto generador, pero antes de hablar más sobre él, explicaremos como obtener los puntos de la curva.
-
Obtener los residuos cuadráticos:
Elementos de p(1-22) mod p Residuo 12 mod 23 1 22 mod 23 4 32 mod 23 9 42 mod 23 16 52 mod 23 2 62 mod 23 13 72 mod 23 3 82 mod 23 18 92 mod 23 12 102 mod 23 8 112 mod 23 6 122 mod 23 6 132 mod 23 8 142 mod 23 12 152 mod 23 18 162 mod 23 3 172 mod 23 13 182 mod 23 2 192 mod 23 16 202 mod 23 9 212 mod 23 4 222 mod 23 1 Tabla 1
Por lo tanto los residuos cuadráticos para son .
-
Para obtener los puntos, vamos a sustituir en la curva los valores de o sea , buscamos si el resultado se encuentra en los residuos cuadráticos obtenidos, si se encuentra entonces en la siguiente columna tenemos la pareja de números con los que obtuvimos ese residuo y en la columna final anotamos la pareja de puntos que son resultado de la combinación del valor de con cada número de la pareja:
x E= y2= x3 + x + 4 mod 23 ¿Se encuentra en RC(23)? Valores con los que se obtuvo el residuo Puntos 0 4 Sí (2,21) (0,2)(0,21) 1 6 Sí (11,12) (1,11)(1,12) 2 14 No () ()() 3 11 No () ()() 4 3 Sí (7,16) (4,7)(4,16) 5 19 No () ()() 6 19 No () ()() 7 9 Sí (3,20) (7,3)(7,20) 8 18 Sí (8,15) (8,8)(8,15) 9 6 Sí (11,12) (9,11)(9,12) 10 2 Sí (5,18) (10,5)(10,18) 11 12 Sí (9,14) (11,9)(11,14) 12 19 No () ()() 13 6 Sí (11,12) (13,11)(13,12) 14 2 Sí (5,18) (14,5)(14,18) 15 13 Sí (6,17) (15,6)(15,17) 16 22 No () ()() 17 12 Sí (9,14) (17,9)(17,14) 18 12 Sí (9,14) (18,9)(18,14) 19 5 No () ()() 20 20 No () ()() 21 17 No () ()() 22 2 Sí (5,18) (22,5)(22,18) Tabla 2
De la tabla se podemos ver que obtuvimos 28 puntos, a estos se les suma un punto que se conoce como punto al infinito, se trata de un elemento neutral que tiene la propiedad: , donde es el punto al infinito.
Otro concepto importante que nace es que se le conoce como orden de la curva al número de puntos que existen, por lo tanto para esta curva decimos que tiene un orden de 29.
Para finalizar es importante hablar sobre el punto generador. El punto generador es un punto con el cual a partir de él se pueden obtener los demás puntos del grupo haciendo uso del doblado y suma de puntos, para ver si un punto es generador o no, lo tomamos y realizamos la operación 2P, si el punto resultado se encuentra dentro de los puntos de la curva, habrá que calcular 3P y así hasta obtener todos los puntos de la curva, si el punto seleccionado nos da un punto que no existe dentro de la curva, habrá que elegir a otro punto y realizar el mismo proceso. Es necesario aclarar que cuando se llegue al último cálculo de estos puntos el resultado se va a indeterminar lo que significa que obtuvimos el punto al infinito().
Dado que el orden de la curva () con la que estaremos trabajando en la animación es primo, nos dice que el grupo con el que decidimos trabajar () es cíclico y cualquier punto es generador de todo el grupo de puntos que calculamos en la tabla 2, para el caso en el que no sea primo habrá que ir probando punto por punto del grupo. El punto seleccionado para trabajar en las animaciones es el (0,2). A continuación en la figura 1 se muestran cómo se obtuvieron todos los puntos de la tabla 2, a partir del (0,2):
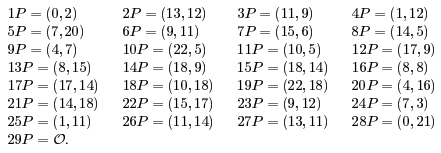
 Referencias
Referencias
- Christof Paar, Jan Pelzl. (2010). Understanding Cryptography. Berlin Heidelberg: Springer.