El cifrado AES es casi idéntico al cifrado de bloques Rijndael. El bloque Rijndael y el tamaño de la clave varían entre 128, 192 y 256 bits. Sin embargo, el estándar AES sólo requiere un tamaño de bloque de 128 bits. Por lo tanto, sólo Rijndael con una longitud de bloque de 128 bits se conoce como el algoritmo AES.

Figura 1: Parámetros de entrada/salida de AES

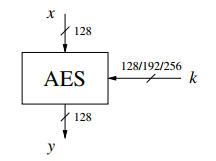
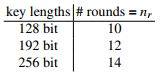
El número de rondas internas del cifrado es en función de la longitud de la clave según la tabla 1.

Tabla 1: Tamaño de llaves y número de rondas para AES

---

Cifrado

A continuación, se examina la estructura interna de AES. La figura 2 muestra la imagen de una sola ronda AES. La entrada de 16 bytes A₀ , ... , A₁₅ se alimenta por bytes en la S-Box. La salida B₀ , ... , B₁₅ de 16 bytes se permuta por bytes en la capa ShiftRows y se mezcla con la transformación C(x) de MixColumn. Finalmente, con la subclave k_i de 128 bits se realiza la operación XOR con el resultado intermedio. Se observa que AES es un cifrado orientado a bytes.

Figura 2: Función de ronda AES para rondas 1, 2,..., n-1

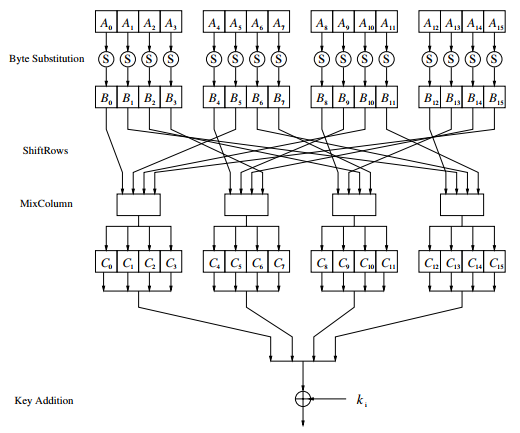
Para entender cómo se mueven los datos a través de AES, primero se imagina que el estado A (es decir, la ruta de datos de 128 bits) que consiste en 16 bytes A₀ , A₁,..., A₁₅ están colocados en un matriz de 4x4 bytes:

Figura 3: Matriz de 4x4 para el estado A

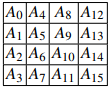
AES opera sobre elementos, columnas o filas de la matriz de estado actual. Del mismo modo, los bytes de la clave están colocados en una matriz con cuatro filas y cuatro (clave de 128 bits), seis (192-bit clave) u ocho (256-bit clave) columnas. Ahora se explicará lo que sucede en cada una de las capas.

Capa de sustitución de bytes

Como se muestra en la figura 4, la primera capa en cada ronda es la capa de sustitución de bytes. La capa de sustitución de bytes se puede ver como una fila de 16 S-Box paralelas, cada una con 8 bits de entrada y salida. En la capa, cada byte de estado A_i se sustituye, es decir, se sustituye por otro byte B_i:

Figura 4: S-Box de AES. Valores de sustitución en notación hexadecimal para cada byte de entrada (xy)

Ejemplo. Supongamos que el byte de entrada a S-Box es A = (C2)_hex, entonces el valor sustituido es:

S((C2)_hex) = (25)_hex

Capa de difusión

En AES, la capa de difusión consta de dos subcapas, la transformación ShiftRows y la transformación MixColumn.

Subcapa ShiftRows

La transformación ShiftRows cambia cíclicamente la segunda fila de la matriz de estado por tres bytes a la derecha, la tercera fila por dos bytes a la derecha y la cuarta por un byte a la derecha. La transformación ShiftRows no cambia la primera fila. Si la entrada de la subcapa ShiftRows se da como una matriz de estado B = (B₀, B₁,..., B₁₅):

Figura 5: Matriz de estado B = (B₀, B₁,..., B₁₅)
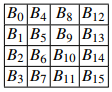
la salida es el nuevo estado:
Figura 6: Matriz de estado después de la capa ShiftRows

Subcapa MixColumn

El paso MixColumn es una transformación lineal que mezcla cada columna de la matriz de estado. En lo que sigue, de denota el estado de entrada de 16 bytes por B y el estado de salida de 16 bytes por C:

donde B es el estado después de ShiftRows.

Ahora, cada columna de 4 bytes se considera como un vector y se multiplica por una matriz 4 × 4 fija. La matriz contiene entradas constantes. La multiplicación y adición de los coeficientes se realiza en GF(2⁸). Como ejemplo, se muestra cómo se calculan los primeros cuatro bytes de salida:

Figura 7: Ejemplo del cálculo de los primeros 4 bytes de salida

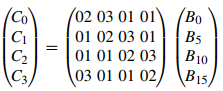
Capa de suma de clave

Las dos entradas de la capa de suma de clave son la matriz de estado actual de 16 bytes y una subclave que también consta de 16 bytes (128 bits). Las dos entradas se combinan mediante una operación XOR bit a bit. Las subclaves se derivan de la generación de claves que se describe a continuación.

Generación de claves

La generación de claves toma la clave de entrada original (de longitud 128, 192 o 256 bits) y obtiene las subclaves utilizadas en AES. El número de subclaves es igual al número de rondas más uno. Por lo tanto, para la longitud de la clave de 128 bits, el número de rondas es n = 10, y hay 11 subclaves, cada una de 128 bits. El AES con clave de 192 bits requiere 13 subclaves de longitud 128 bits, y AES con una clave de 256 bits tiene 15 subclaves.

Las 11 subclaves se almacenan en una matriz de expansión de claves con los elementos W[0],..., W[43]. Las subclaves se calculan como se muestra en la figura 8. Los elementos K₀,..., K₁₅ indican los bytes de la clave AES original. En primer lugar, observamos que la primera subclave k₀ es la clave AES original, es decir, la clave se copia en los primeros cuatro elementos de la matriz de claves W. Los otros elementos de la matriz se calculan de la siguiente manera.

Figura 8: Generación de claves AES para un tamaño de clave de 128 bits

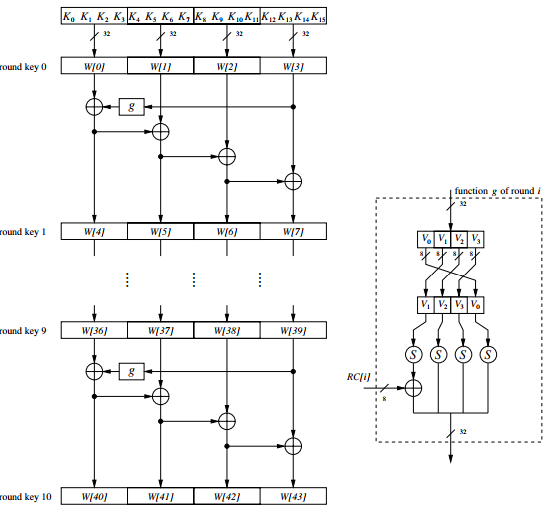
Como se puede ver en la figura, la palabra más a la izquierda de una subclave W[4i], donde i = 1,..., 10, se calcula como:

Aquí g( ) es una función no lineal con una entrada y salida de cuatro bytes. Las tres palabras restantes de una subclave se calculan recursivamente como:

donde i = 1 , ... , 10 y j = 1, 2, 3. La función g( ) gira sus cuatro bytes de entrada, realiza una sustitución de bytes usando la S-Box y le añade un coeficiente de ronda RC. El coeficiente es un elemento del campo de Galois GF(2⁸), es decir, un valor de 8 bits. Sólo se agrega al byte más a la izquierda en la función g(). Los coeficientes varían según la siguiente regla:

RC[1] = x⁰ = (00000001)₂,
RC[2] = x¹ = (00000010)₂,
RC[3] = x² = (00000100)₂,
.
.
.
RC[9] = x⁹ = (000110011)₂,
RC[10] = x⁹ = (00110110)₂.

La función g() tiene dos propósitos. En primer lugar, añade no linealidad a la generación de llaves. En segundo lugar, elimina la simetría en AES. Ambas propiedades son necesarias para frustrar ciertos ataques de cifrado de bloque.

---

Descifrado

Debido a que AES no está basado en una red Feistel, todas las capas deben invertirse, es decir, la capa de sustitución de bytes se convierte en la capa de sustitución Byte Inv, la capa ShiftRows se convierte en la capa Inv ShiftRows y la capa MixColumn se convierte en la capa Inv MixColumn. Sin embargo, resulta que las operaciones de capa inversa son bastante similares a las operaciones de capa utilizadas para el cifrado. Además, el orden de las subclaves se invierte, es decir, se necesita una generación de claves de forma invertida. En la figura 9 se muestra un diagrama de bloques de la función de descifrado.

Figura 9: Diagrama de bloques de descifrado AES

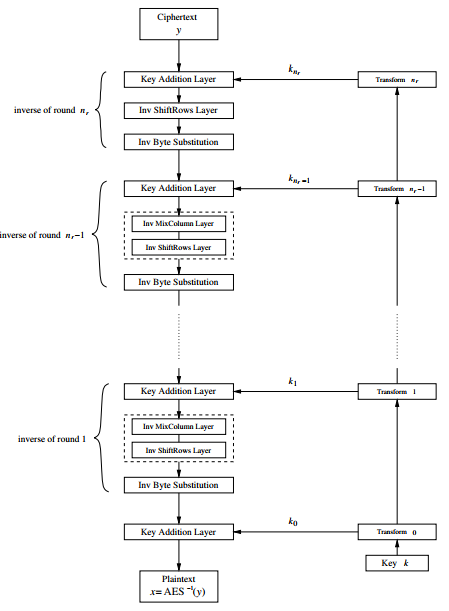
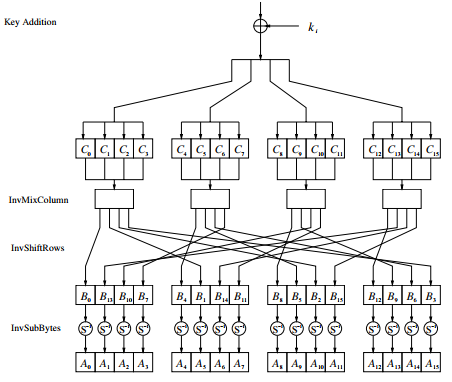
Dado que la última ronda de cifrado no realiza la operación MixColum, la primera ronda de descifrado tampoco contiene la capa inversa correspondiente. Todas las demás rondas de descifrado, sin embargo, contienen todas las capas AES. En lo que sigue, se discuten de forma general las capas inversas de la ronda de descifrado AES (Figura 10). Dado que la operación XOR es su propia inversa, la capa de suma de clave en el modo de descifrado es la misma que en el modo de cifrado.

Figura 10: Función de ronda para descifrado AES para rondas 1, 2,..., n_r -1

Capa MixColum inversa

Después de la suma de la subclave, el paso de la función inversa de MixColumn se aplica al estado (de nuevo, la excepción es la primera ronda de descifrado). Para invertir la operación MixColumn, debe usarse la inversa de su matriz. La entrada es una columna de 4 bytes del estado C que se multiplica por la matriz inversa 4 × 4. La matriz contiene entradas constantes. La multiplicación y adición de los coeficientes se realiza en GF (2⁸).

Figura 11: Multiplicación con la matríz inversa

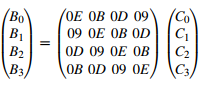
Las sumas en la multiplicación vector-matriz son XORs bit a bit.

Capa ShiftRows inversa

Para invertir la operación ShiftRows del algoritmo de cifrado, debemos desplazar las filas de la matriz de estado en la dirección opuesta. La primera fila no cambia por la transformación inversa ShiftRows. Si la entrada de la subcapa ShiftRows se da como una matriz de estado B = (B₀ , B₁,..., B₁₅):

Figura 12: Matriz de estado B = (B₀ , B₁ ,..., B₁₅)

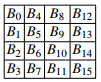
La subcapa inversa ShiftRows produce la salida:

Figura 13: Matriz de estado después de la capa inversa ShiftRows

Capa Sustitución de bytes inversa

La S-Box inversa se utiliza al descifrar un texto cifrado. Dado que la S-Box de AES es una correspondencia bijectiva, es decir, uno a uno, es posible construir una S-Box inversa tal que:

Donde A_I y B_i son elementos de la matriz de estado. Las entradas de la S-Box inversa se dan en la figura 14:

Figura 14: S-Box inversa de AES. Valores de sustitución en notación hexadecimal para cada byte de entrada (xy)

Generación de claves para el descifrado

Dado que la primer ronda de descifrado necesita la última subclave, la segunda ronda de descifrado necesita la penúltima subclave generada durante el cifrado y así sucesivamente, necesitamos las subclaves en orden inverso como se muestra en la figura 9. En la práctica, esto se logra principalmente calculando primero toda la generación de claves y almacenando todas las 11, 13 o 15 subclaves, dependiendo del número o rondas que utiliza AES (que a su vez depende de las tres longitudes de clave soportadas por AES).

---

Referencias

1. Paar C., Pelzl J.. (2010). Understanding Cryptography. Nueva York: Springer-Verlag Berlin Heidelberg. pp.87-118