El algoritmo Secure Hash (SHA-1) es la función de resumen de mensajes más utilizada de la familia MD4. Aunque se han propuesto nuevos ataques contra el algoritmo, es muy instructivo mirar sus detalles porque las versiones más fuertes en la familia SHA-2 muestran una estructura interna muy similar.

Las rondas de SHA-1 son bastante similares a un cifrado de bloques Feistel.

SHA-1 produce una salida de 160 bits de un mensaje con una longitud máxima de 2⁶⁴ bits. Antes del cálculo del hash, el algoritmo tiene que preprocesar el mensaje.

Preprocesamiento

Antes del cálculo de hash real, el mensaje X tiene que ser rellenado para ajustarse a un tamaño de un múltiplo de 512 bits. Para el procesamiento interno, el mensaje rellenado debe entonces dividirse en bloques. Además, el valor inicial H₀ se establece en una constante predefinida.

Padding

Supongamos que tenemos un mensaje X con una longitud de l bits. Para obtener un tamaño de mensaje global de un múltiplo de 512 bits, añadimos un "1" seguido de k bits cero y la representación binaria de 64 bits de l. Por consiguiente, el número de ceros requeridos k viene dado por:

La figura 1 ilustra el relleno de un mensaje x.

Figura 1: Relleno de un mensaje X

Ejemplo 1. Dado el mensaje abc que consta de tres caracteres ASCII de 8 bits con una longitud total de l = 24 bits:

Figura 2: Representación binaria de "abc"

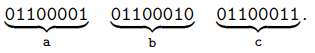
Agregamos un "1" seguido de k = 423 bits cero, donde k está determinado por:

k ≡ 448−(l +1) = 448−25 = 423 mod 512

Finalmente, añadimos el valor de 64 bits que contiene la representación binaria de la longitud l = 24₁₀ = 11000₂. El mensaje rellenado es entonces dado por:

Figura 3: Relleno de un mensaje

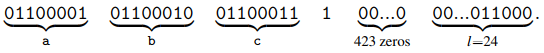
Dividir el mensaje rellenado

Antes de aplicar la función de compresión, se necesita dividir el mensaje en bloques de 512 bits x₁, x₂ , ... , x_n. Cada bloque de 512 bits se puede subdividir en 16 palabras de tamaño de 32 bits. Por ejemplo, el i-ésimo bloque del mensaje x se divide en:

donde x_i^(k) son palabras de 32 bits.

Valor inicial H₀

Se utiliza un búfer de 160 bits para contener el valor de hash inicial para la primera iteración. Las cinco palabras de 32 bits son fijas y se dan en notación hexadecimal:

A= H₀⁽⁰⁾= 67452301
B= H₀⁽¹⁾= EFCDAB89
C= H₀⁽²⁾= 98BADCFE
D= H₀⁽³⁾= 10325476
E= H₀⁽⁴⁾= C3D2E1F0

Cálculo Hash

Cada bloque de mensajes x_i se procesa en cuatro etapas con 20 rondas cada una como se muestra en la Figura 5. El algoritmo utiliza:

1. Un programa de mensajes que calcula una palabra de 32 bits W₀ , W₁ , ... , W₇₉ para cada una de las 80 rondas. Las palabras W_j se derivan del bloque de mensaje de 512 bits como sigue:
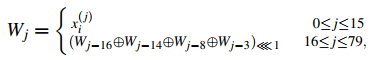
   Figura 4
   Donde X_<<<n indica un desplazamiento circular a la izquierda de la palabra X por n posiciones de bit.
2. Cinco registros de trabajo de tamaño de 32 bits: A, B, C, D, E
3. Un valor de hash H_i que consta de cinco palabras de 32 bits H_i⁽⁰⁾, H_i⁽¹⁾, H_i⁽²⁾, H_i⁽³⁾, H_i⁽⁴⁾. Al principio, el valor hash contiene el valor inicial H₀, que se sustituye por un nuevo valor hash después del procesamiento de cada bloque de mensaje. El valor final hash H_n es igual a la salida h(x) de SHA-1.

Figura 5

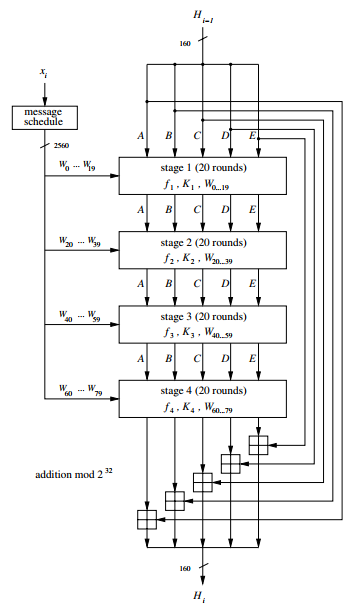
Las cuatro etapas SHA-1 tienen una estructura similar pero utilizan diferentes funciones internas f_t y constantes K_t, donde 1 ≤ t ≤ 4. Cada etapa está compuesta de 20 rondas, donde partes del bloque de mensajes son procesadas por la función f_t junto con algunas constantes dependientes de la etapa K_t. La salida después de 80 rondas se agrega al valor de entrada H_i-1 módulo 2³² en forma de palabras.

La operación de la ronda j en la etapa t viene dada por:

Figura 6

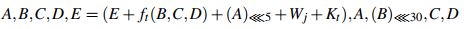
Y como se muestra en la figura 7. Las funciones internas f_t y constantes K_t cambian:

Figura 7

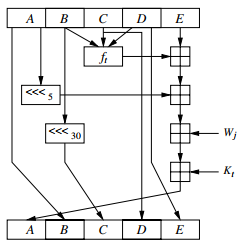
Dependiendo de la etapa de acuerdo con la Tabla 1, es decir, cada 20 rondas se está utilizando una nueva función y una nueva constante. La función sólo utiliza operaciones booleanas bit a bit, es decir, AND lógico (∧), OR (∨), NOT (barra superior) y XOR. Estas operaciones se aplican a variables de 32 bits y son muy rápidas de implementar en PCs modernas.

Tabla 1

Referencias

1. Paar C., Pelzl J.. (2010). Understanding Cryptography. Nueva York: Springer-Verlag Berlin Heidelberg. pp.307-311