Cifrado Hill

Lester S. Hill
Este sistema de cifrado está basado en el álgebra lineal y ha sido importante en la historia de la criptografía. Fue inventado por Lester S. Hill en 1929, y fue el primer sistema criptográfico polialfabético que era práctico para trabajar con más de tres símbolos simultáneamente.
Este sistema es polialfabético, esto quiere decir que puede darse que un mismo carácter en un mensaje a enviar se encripte en dos caracteres distintos en el mensaje encriptado.
Suponiendo que trabajamos con el alfabeto español de 27 caracteres, las letras se numeran en orden alfabético de forma tal que A=0, B=1,..., Z=26.
Se elige un entero que determina bloques de elementos que son tratados como un vector de dimensiones.
Se elige de forma aleatoria una matriz de elementos los cuales serán la llave del sistema a utilizar.
Los elementos de la matriz de serán enteros entre 0 y 26 y la matriz de cifrado debe ser invertible en Z27.

Cifrado
Para realizar el cifrado del mensaje, se elige un número entero y el texto es dividido en bloques de elementos los cuales se multiplican por la matriz de cifrado de tamaño la cual es elegida aleatoriamente, tomando en cuenta que la matriz de cifrado debe ser invertible en Z27.
Por ejemplo:
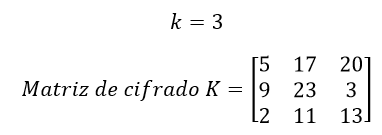
Para cifrar el mensaje codigo debemos cifrar los seis caracteres de codigo en bloques de caracteres cada uno.
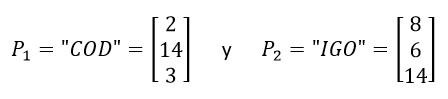
Posteriormente, las matrices correspondientes al mensaje son multiplicadas cada una de ellas por la matriz de cifrado, la cual es la llave del sistema.
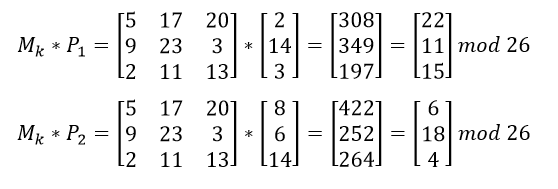
El primer bloque se cifraría como BUS y el segundo como KMH, dando como resultado BUSKMH como el texto cifrado correspondiente para el mensaje en claro codigo.
Observar que las dos O se codificaran de forma diferente.

Descifrado
Para realizar el descifrado del mensaje, se elige un número entero y el cifrado es dividido en bloques de elementos los cuales se multiplican por la matriz de descifrado de tamaño la cual es obtenida de la matriz de cifrado elegida aleatoriamente, tomando en cuenta que la matriz de cifrado debe ser invertible en Z27, de lo contrario, la matriz de descifrado no sería útil.
Por ejemplo:

Se verifica que la matriz elegida es invertible en módulo 27. Una forma sencilla es calcular el determinante de la matriz. Si el determinante es 0 o tiene factores en común con el módulo 27, que es el 3, entonces la matriz no puede utilizarse. Esto quiere decir que todas las matrices que su determinante sea 0 o un múltiplo de 3, no servirán.
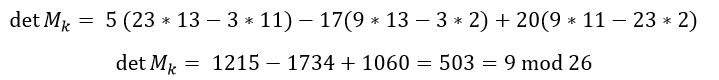
La matriz es invertible en módulo 27 ya que 27 y 17 son coprimos.
Para hallar la inversa de la matriz módulo 27, utilizamos la formula
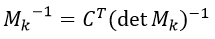
Dónde es la matriz de cofactores de transpuesta.
Hay que tener en cuenta que debe realizarse en módulo 27, por lo tanto, para el ejemplo la inversa de 17 es 8 mod 27.
Se calcula .
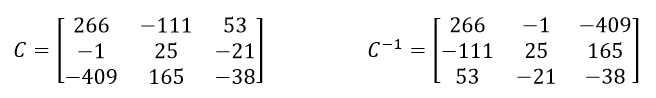
Ahora podemos aplicar la fórmula de la inversa
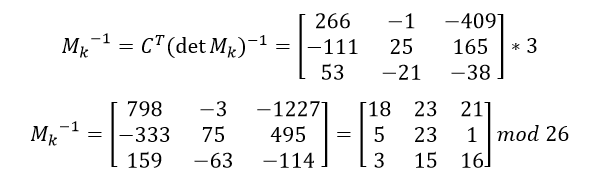
Esta última es la matriz que utilizamos para descifrar.
Para descifrar el mensaje BUSKMH debemos descifrar los seis caracteres de BUSKMH en bloques de caracteres cada uno.
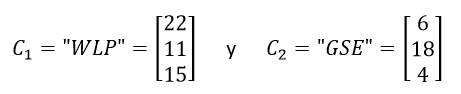
Posteriormente, las matrices correspondientes al cifrado son multiplicadas cada una de ellas por la matriz de descifrado.
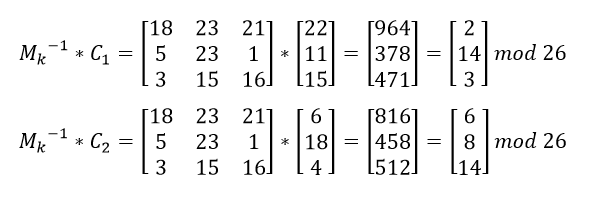
El primer bloque se descifra como cod y el segundo como igo, dando como resultado codigo como el mensaje en claro.
 Referencias
Referencias
- Douglas Stinson. (1995). Cryptography: Theory and Practice. United States: CRC Press.
- Wade Trappe, Lawrence C. Washington. (2006). Introduction to Cryptography with Coding Theory. United States: Prentice Hall.